数据结构基础知识体系详解

提示

本文讨论的数据结构都是以C++语言来实现

知识体系

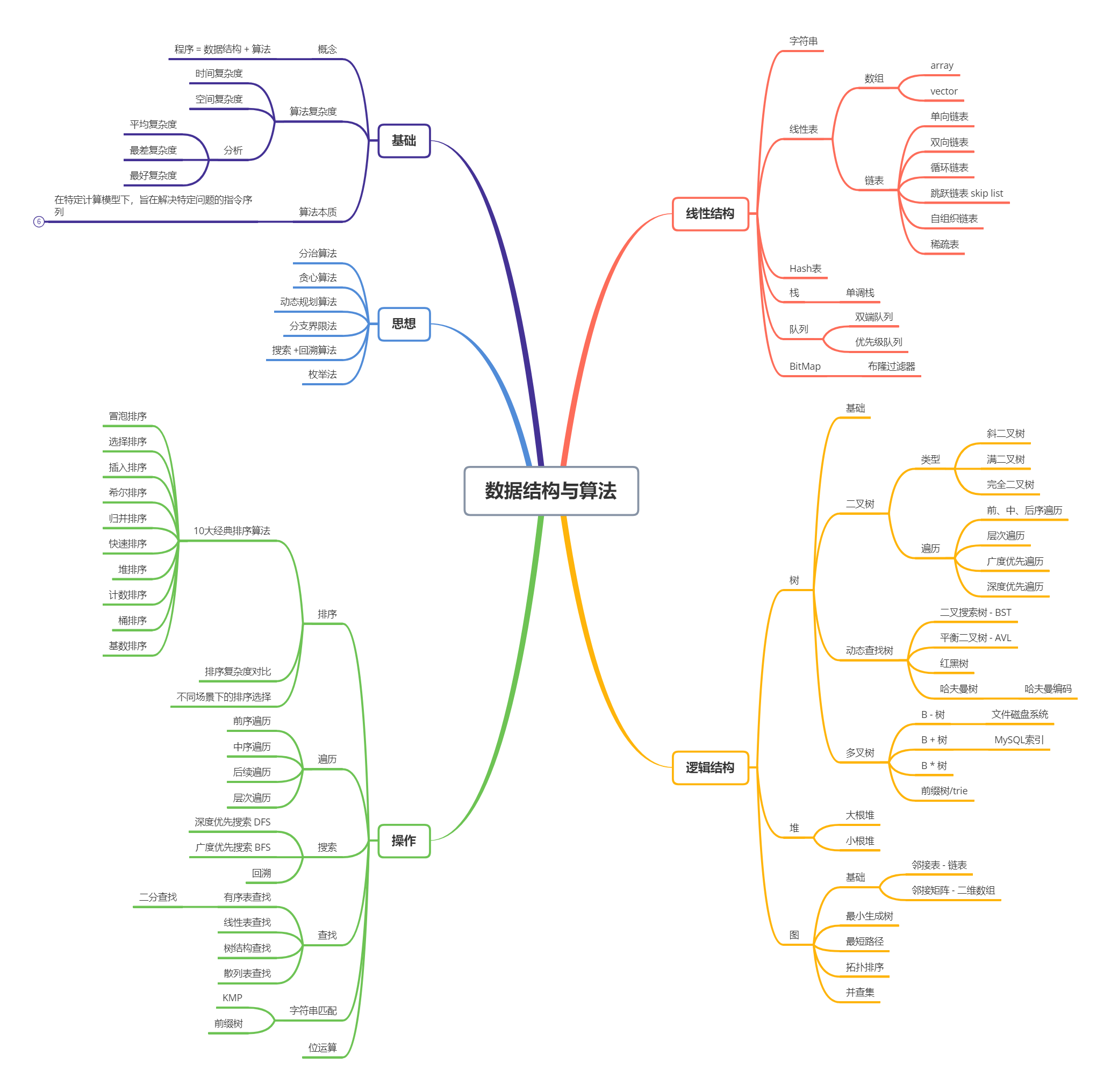
数据结构与算法

数据结构的存储⽅式只有两种：数组（顺序存储）和链表（链式存储）。

对于散列表、栈、队列、堆、树、图等等各种数据结构，抽象化后都可以用链表或者数组上的特殊操作来实现，仅API不同而已。

引申STL中的双端队列deque,由其为底层结构可以通过封闭头部开口实现栈stack，封闭头部入口，尾部出口实现queue。

队列，栈这两种数据结构既可以使⽤链表也可以使⽤数组实现。数组实现，就要处理扩容缩容的问题；链表实现，没有这个问题，但需要更多的内存空间存储节点指针。
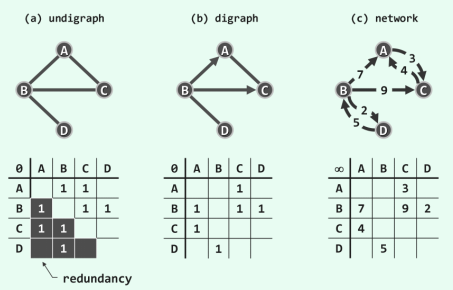
图的两种表方法，邻接表就是链表，邻接矩阵就是二维数组。邻接矩阵判断连通性迅速，并可以进矩阵运算解决些问题，但是如果图⽐较稀疏的话很耗费空间。邻接表比较节省空间，但是很多操作的效率上肯定比不过邻接矩阵。
- 邻接表
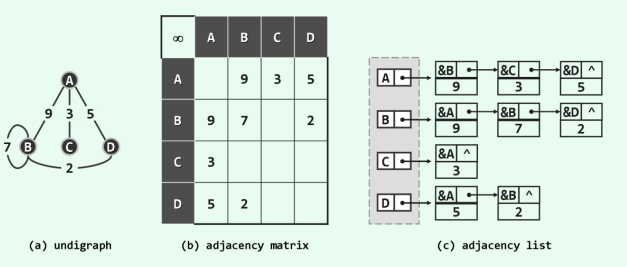
- 邻接矩阵
散列表。hashfuntion可以将某一元素映射为一个“大小可接受之索引”，即大数映射成小数。hashtable通过hashfunction将元素映射到不同的位置，但当不同的元素通过hash function映射到相同位置时，便产生了＂碰撞＂问题．
- 解决碰撞问题的方法主要有线性探测，二次探测，开链法等．
树，因为不一定是完全二叉树，所以不适合用数组存储。为此，在这种链表「树」结构之上，又衍生出各种巧妙的设计，例如二叉搜索树、 AVL树、红黑树、区间树、 B 树等等，以应对不同的问题。

综上，数据结构种类很多，甚至可以自定义新的数据结构，但是其底层存储无非是数组或者链表，两者的优缺点如下：

数组由于是紧凑连续存储，可以随机访问，通过索引快速找到对应元素，而且相对节约存储空间。
- 但正因为连续存储，内存空间必须一次性分配够，所以说数组如果要扩容，需要重新分配一块更大的空间，再把数据全部复制过去，时间复杂度 O(N)。
- 数组中间进行插入或删除，每次必须搬移后面的所有数据以保持连续，时间复杂度 O(N)。
链表因为元素不连续，而是靠指针指向下一个元素的位置，所以不存在数组的扩容问题。
- 根据某个元素的前驱和后驱，操作指针即可删除该元素或插入新元素，时间复杂度 O(1)。