领域算法 - 布隆过滤器
布隆过滤器(Bloom Filter)是由一个很长的bit数组和一系列哈希函数组成的。本质上是一种数据结构,比较巧妙的概率型数据结构。它的特点是高效地插入和查询,并且根据查询结果可以知道某样东西一定不存在或者可能存在。相比于传统的 List、Set、Map 等数据结构,它更高效、占用空间更少,但是缺点是其返回的结果是概率性的,而不是确切的,同时布隆过滤器还有一个缺陷就是数据只能插入不能删除。
布隆过滤器的实现思路
设数据集合A={a1,a2,a3,...,an},含有n个元素作为待操作的集合;
Bloom Filter用一个长度为m的位向量V表示集合中的元素,位向量初始值全为0;
k个具有均匀分布特性的散列函数h1,h2,...,hk;
对于要加入的元素,首先经过k个散列函数%m,产生k个随机数h1,h2,...,hk,使向量V的相应位置h1,h2,...,hk均置位为1。集合中其他元素也通过类似的操作,将向量V的若干位置为1;
对于新要加入的元素的检查,首先将该元素经过上步中类似的操作,获取k个随机数h1,h2,...,hk,然后查看向量V的相应位置h1,h2,...,hk上的值,若全为1,则该元素已经在之前的集合中;若至少有一个0存在,表明此元素不在之前的集合中,为新元素。
特点:
对于已经在集合中的元素,通过⑤中的查找方法,一定可以判定该元素在集合中;对于不在集合中的元素,可能会被误判在集合中。
布隆过滤器的公式
布隆过滤器的大小m公式,其中n为样本个数,p为误判率:
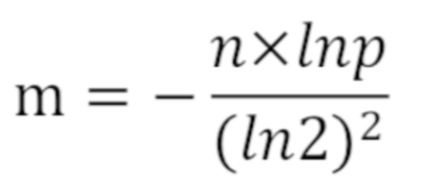
哈希函数的个数k公式:

布隆过滤器真实失误率p公式:

实际应用场景
背景:现在有个100亿个黑名单网页数据,每个网页的URL占用64字节。现在想要实现一种网页过滤系统,可以根据网页的URL判断该网站是否在黑名单上,请设计该系统。
需求:可以允许有0.01%以下的判断失误率,并且使用的总空间不要超过200G。
提取关键信息:100亿条黑名单数据,每条数据占64个字节,万分之一的失误率,总空间不要超过200G。
分析:如果不考虑不布隆过滤器,那么这里存储100亿条数据就需要 100亿 * 64字节 = 596G 显然超过300G
解题:在满足有 100亿条数据 并且允许 万分之一的失误率 的布隆过滤器需要多大的bit数组呢?
设bit数组大小为m,样本数量为n,失误率为p。
由题可知 n = 100亿,p = 0.01% 根据布隆过滤器的大小m公式,求得 m = 19.19n,向上取整为 20n。所以2000亿bit,约为186G。 根据哈希函数的个数k公式,求得 k = 14,即需要14个哈希函数。 通过 上述计算得到的 m = 20n, k = 14 ,根据布隆过滤器真实失误率p公式,求得 p = 0.006%。