回溯算法

• 回溯算法
  • 实践应用
    • 例题 46. 全排列

Backtrack是DFS的一种形式，基本写法类似于Top Down DFS,但是引入了状态回溯。

核心思想：每次搜索一个分支，会首先记录当前节点的状态，尝试某一分支后，把状态回溯到记录的状态，再去尝试另外的分支。

模板:

Backtrack()

1. Base Case
2. For each possiblity possiblity
    a. memorize current state
    b. backtrack(next_state)
    c. restore current state

引申：

全排列和全排列2

实践应用

例题 46. 全排列

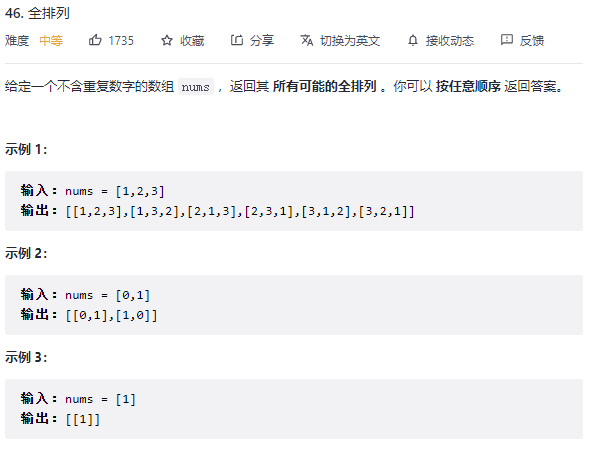
以下为解题代码：

class Solution {
public:
    void backtrack(vector<vector<int>>& res, vector<int>& output, int first, int len){
        // 所有数都填完了
        if (first == len) {
            res.emplace_back(output);
            return;
        }
        for (int i = first; i < len; ++i) {
            // 动态维护数组
            swap(output[i], output[first]);
            // 继续递归填下一个数
            backtrack(res, output, first + 1, len);
            // 撤销操作
            swap(output[i], output[first]);
        }
    }
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int> > res;
        backtrack(res, nums, 0, (int)nums.size());
        return res;
    }
};