C++ 全栈知识体系

数组题型

全排列

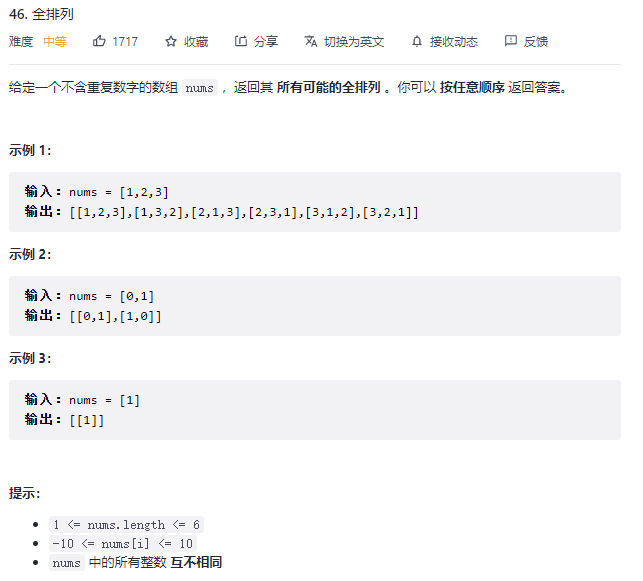
题解：

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;

        if(nums.size()==0){
            return res;
        }

        int size=nums.size();
        int depth=0;
        vector<bool> isUsed(size,false);
        vector<int> tmpRes;

        dfs(nums,size,depth,isUsed,tmpRes,res);

        return res;
    }

    void dfs(vector<int>& nums,int size,int depth,vector<bool> isUsed,vector<int> tmpRes,vector<vector<int>>& res){
        if(depth==size){
            res.push_back(tmpRes);
        }

        for(int i=0;i<size;i++){
            if(isUsed[i]){
                continue;
            }
            isUsed[i] =true;
            tmpRes.push_back(nums[i]);
            dfs(nums,size,depth+1,isUsed,tmpRes,res);
            isUsed[i] =false;
            tmpRes.pop_back();
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

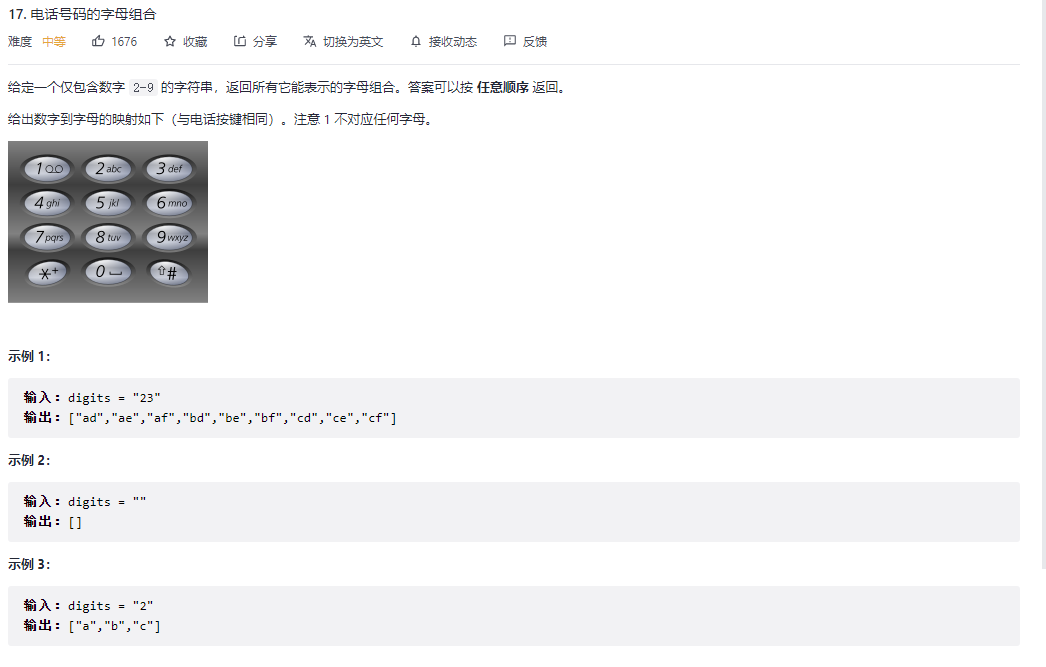
电话号码的字母组合

class Solution {
public:
    string tmp;
    vector<string> res;
    vector<string> board={"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};
    void DFS(int pos,string digits){
        if(pos==digits.size()){
            res.push_back(tmp);
            return;
        }
        int num=digits[pos]-'0';
        for(int i=0;i<board[num].size();i++){
            tmp.push_back(board[num][i]);
            DFS(pos+1,digits);
            tmp.pop_back();
        }
    }
    vector<string> letterCombinations(string digits) {
        if(digits.size()==0) return res;
        DFS(0,digits);
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

技巧:可以采用广度优先遍历和深度优先遍历

盛最多水的容器

盛最多水的容器

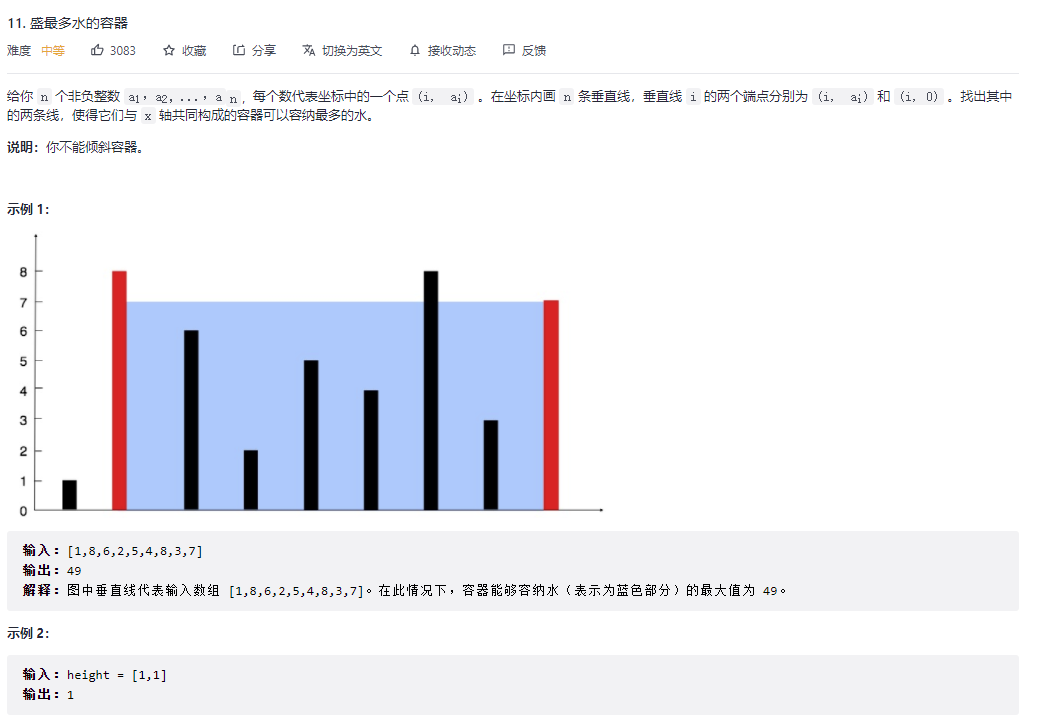
采用双指针解法：每次移动短边。

class Solution {
public:
    int maxArea(vector<int>& height) {
        int maxArea=-1;
        int size=height.size();
        int left=0;
        int right=size-1;

        while(left<right){
            if(height[left]<height[right]){
                maxArea=max(maxArea,height[left]*(right-left));
                left++;
            }
            else {
                maxArea=max(maxArea,height[right]*(right-left));
                right--;
            }
        }

        return maxArea;

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
  1. 打家劫舍
class Solution {
public:
    int maxSum=0;
    int rob(vector<int>& nums) {
        int size=nums.size();
        int curSum=0;
        backtrack(0,size,nums,curSum);

        return maxSum;
    }

    void backtrack(int pos,int size,vector<int>& nums,int curSum){
        if(pos>=size){
            maxSum =max(maxSum,curSum);
        }

        for(int i=pos;i<size;i++){
            backtrack(i+2,size,nums,curSum + nums[i]);
            backtrack(i+1,size,nums,curSum);
        }

    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
  1. 数组中的第K个最大元素
class Solution {
public:
    int findKthLargest(vector<int>& nums, int k) {
        priority_queue<int> queue;

        for(int i=0;i<nums.size();i++){
            queue.emplace(nums[i]);
        }

        for(int i=0;i<=k-1;i++){
            if(i==k-1)
                return queue.top();
            queue.pop();
        }
        return 0;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
  1. 除自身以外数组的乘积

注意边界

class Solution {
public:
    vector<int> productExceptSelf(vector<int>& nums) {
        int size=nums.size();
        int left=0,right=size-1;

        int leftSum=1;
        int rightSum=1;

        vector<int> afterVec(size,1);
        vector<int> preVec(size,1);
    

        for(int i=right;i>0;i--){
            rightSum=rightSum*nums[i];
            afterVec[i]=rightSum;
        }

        for(int i=0;i<right;i++){
            leftSum=leftSum*nums[i];
            preVec[i]=leftSum;
        }

        for(int i=0;i<=right;i++){
            if(i-1>=0&&i+1<=right)
                nums[i]=preVec[i-1]*afterVec[i+1];
            else if(i==0){
                nums[i]=afterVec[i+1];
            }
            else if(i==right){
                nums[i]=preVec[i-1];
            }
        }

        return nums;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
  1. 前 K 个高频元素
class Solution {
public:

    static bool cmp_by_value(const pair<int,int> & lhs, const pair<int,int> & rhs) {
        return lhs.second > rhs.second;
    }

    vector<int> topKFrequent(vector<int>& nums, int k) {
            map<int,int> mp;
            vector<int> res;

            for(int i=0;i<nums.size();i++){
                if(mp.count(nums[i])){
                    mp[nums[i]]++;
                }
                else{
                    mp[nums[i]]=1;
                }
            }

            vector<pair<int,int>> tmp;

            for(map<int,int>::iterator iter=mp.begin();iter!=mp.end();iter++){
                tmp.push_back({iter->first,iter->second});
            }

            sort(tmp.begin(),tmp.end(),cmp_by_value);

            for(int i=0;i<tmp.size()&&k>0;i++,k--){
                res.push_back(tmp[i].first);
            }
            
            return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
  1. 目标和
class Solution {
public:
    int res=0;
    int findTargetSumWays(vector<int>& nums, int target) { 
        backtrack(nums,target,0,0);
        return res;
    }

    void backtrack(vector<int>& nums, int target, int pos,int cur){
        if(pos==nums.size()){
            if(cur==target)
                res++; 
            return;
        }

        backtrack(nums,target,pos+1,cur-nums[pos]);
        backtrack(nums,target,pos+1,cur+nums[pos]);
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
  1. 滑动窗口最大值
class Solution {
public:
    vector<int> maxSlidingWindow(vector<int>& nums, int k) {
        priority_queue<pair<int,int>> heap;
        vector<int> res;
        int left=0;

        for(int i=0;i<k;i++){
            heap.push({nums[i],i});
        } 

        res.push_back((heap.top()).first);

        for(int i=k;i<nums.size();i++){
            heap.push({nums[i],i});
            
            while(heap.top().second<=i-k){
                heap.pop();
            }

            res.push_back(heap.top().first);
        } 
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

240. 搜索二维矩阵 II (opens new window)

class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m=matrix.size();
        int n=matrix[0].size();

        for(int i=0;i<m;i++){
            if(target>matrix[i][n-1] || target<matrix[i][0]){
                continue;
            }

            if(binSearch(matrix[i],target)){
                return true;
            }
            
        }

        return false;
    }

    bool binSearch(vector<int>& nums,int target){
        int left=0,right=nums.size()-1;

        while(left<=right){
            int mid=left +(right-left)/2;

            if(nums[mid]==target){
                return true;
            }
            else if(nums[mid]<target){
                left=mid+1;
            }
            else{
                right=mid-1;
            }
        }

        return false;
    }
};

最优解:Z 字形查找
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        int m=matrix.size();
        int n=matrix[0].size();

        int row=0,col=n-1;

        while(row<m && col>=0){
            if(matrix[row][col]==target)
                return true;
            
            if(matrix[row][col]<target){
                row++;
            }
            else if(matrix[row][col]>target){
               col--;
            }
        }

        return false;
    }

};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66

84. 柱状图中最大的矩形 (opens new window)

暴力解:
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int n = heights.size();
        int ans = 0;
        // 枚举左边界
        for (int left = 0; left < n; ++left) {
            int minHeight = INT_MAX;
            // 枚举右边界
            for (int right = left; right < n; ++right) {
                // 确定高度
                minHeight = min(minHeight, heights[right]);
                // 计算面积
                ans = max(ans, (right - left + 1) * minHeight);
            }
        }
        return ans;
    }
};

单调栈：
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int len = heights.size();
        if (len == 0) {
            return 0;
        }
        if (len == 1) {
            return heights[0];
        }

        int res = 0;
		stack<int> stack;
        for (int i = 0; i < len; i++) {
            // 这个 while 很关键，因为有可能不止一个柱形的最大宽度可以被计算出来
            while (!stack.empty() && heights[i] < heights[stack.top()]) {
                int curHeight = heights[stack.top()];
				stack.pop();
                while (!stack.empty() && heights[stack.top()] == curHeight) {
                    stack.pop();
                }

                int curWidth;
                if (stack.empty()) {
                    curWidth = i;
                } else {
                    curWidth = i - stack.top() - 1;
                }

                // System.out.println("curIndex = " + curIndex + " " + curHeight * curWidth);
                res = max(res, curHeight * curWidth);
            }
            stack.push(i);
        }

        while (!stack.empty()) {
            int curHeight = heights[stack.top()];
			stack.pop();
            while (!stack.empty() && heights[stack.top()] == curHeight) {
				stack.pop();
            }
            int curWidth;
            if (stack.empty()) {
                curWidth = len;
            } else {
                curWidth = len - stack.top() - 1;
            }
            res = max(res, curHeight * curWidth);
        }
        return res;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74

560. 和为 K 的子数组 (opens new window)

class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count=0;

        for(int i=0;i<nums.size();i++){
            int curSum=0;
            for(int j=i;j<nums.size();j++){
                curSum=curSum+nums[j];
                if(curSum==k)
                    count++;
            }
        }

        return count;
    }
};

前缀和 + 哈希表优化
    
class Solution {
public:
    int subarraySum(vector<int>& nums, int k) {
        int count=0;
        unordered_map<int,int> mp;
        mp[0]=1;

        int preSum=0;
        for(int i=0;i<nums.size();i++){
            preSum+=nums[i];

            if(mp.count(preSum-k)){
                count+=mp[preSum-k];
            }

            mp[preSum]++;
        }

        return count;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

581. 最短无序连续子数组 (opens new window)


有些情况不对：
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        //查找逆序对
        int begin=-1,end=-1;
        for(int i=0;i<nums.size()-1;i++){
            if(begin==-1&&nums[i]>nums[i+1]){
                begin=i;
                end=i+1;
            }

            if(nums[i]>nums[i+1]){
                end=i+1;
            }
            else if(nums[i]==nums[i+1]){
                if(nums[begin]>nums[i+1]){
                   end=i+1; 
                }
            }
        }

        if(begin==-1){
            return 0;
        }

        return end-begin+1;
    }
};

找出左右两边已经排序的子数组，然后通过size-left-right 计算。
    
class Solution {
public:
    int findUnsortedSubarray(vector<int>& nums) {
        vector<int> tmp=nums;
        int size=nums.size();

        sort(tmp.begin(),tmp.end());

        if(tmp==nums)
            return 0;

        int left=0,right=0;
        for(int i=0;i<size;i++){
            if(tmp[i]!=nums[i]){
                break;
            }
            left++;
        }

        for(int i=size-1;i>=0;i--){
            if(tmp[i]!=nums[i]){
                break;
            }
            right++;
        }

        return size-left-right;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62

416. 分割等和子集 (opens new window)

class Solution {
public:
    bool isFind=false;
    bool canPartition(vector<int>& nums) {
        int sum=0;
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
        }

        if(sum%2==1)
            return false;

        int target=sum/2;

        backtrack(0,0,target,nums);
        return isFind;
    }
    

    void backtrack(int pos,int curSum,int target,vector<int>& nums){
        if(isFind)
            return;

        if(pos==nums.size()){
            isFind=false;
        }
        else{
            if(curSum==target && pos!=0){
                isFind=true;
            }
            backtrack(pos+1,curSum+nums[pos],target,nums);
            backtrack(pos+1,curSum,target,nums);
        }
    }
};

加记忆：
class Solution {
public:
    bool isFind=false;
    map<string,bool> mp;
    bool canPartition(vector<int>& nums) {
        int sum=0;
        for(int i=0;i<nums.size();i++){
            sum+=nums[i];
        }

        if(sum%2==1)
            return false;

        int target=sum/2;

        backtrack(0,0,target,nums);
        return isFind;
    }
    

    void backtrack(int pos,int curSum,int target,vector<int>& nums){
        if(isFind)
            return;

        if(pos==nums.size()){
            isFind=false;
        }
        else{
            if(curSum==target && pos!=0){
                isFind=true;
            }
            string key=std::to_string(pos)+"&"+std::to_string(curSum);
            if(mp.count(key)){
                isFind=mp[key]; 
            }
            else{
                backtrack(pos+1,curSum+nums[pos],target,nums);
                backtrack(pos+1,curSum,target,nums);
                mp[key]=isFind; 
            }
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80

31. 下一个排列 (opens new window)

class Solution {
public:
    /*
    1.从后往前找到第一个破坏单调递增性质的位置(x,y)
    2.将nums[x]与nums[y,n)中比nums[x]大的最小数交换位置
    3.nums[y,n)f反转

    24534421
    24541234
    */
    void nextPermutation(vector<int>& nums) {
        int size=nums.size();

        if(size<2)
            return;
        
        int i=size-2;
        while(i>=0 && nums[i]>=nums[i+1]){
            i--;
        }

        if(i>=0){
            int j=size-1;

            while(j>=0 && nums[i]>=nums[j]){
                j--;
            }
            swap(nums[i],nums[j]);
        }

        reverse(nums.begin()+i+1,nums.end());
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

42. 接雨水 (opens new window)

//直接按问题描述进行。对于数组中的每个元素，我们找出下雨后水能达到的最高位置，等于两边最大高度的较小值减去当前高度的值。
class Solution {
public:
    int trap(vector<int>& height) {
        int ans=0;
        int size=height.size();

        for(int i=1;i<size-1;i++){
            int left_max=0,right_max=0;

            for(int l=i;l>=0;l--){
                left_max=max(left_max,height[l]);
            }

            for(int r=i;r<size;r++){
                right_max=max(right_max,height[r]);
            }

            ans=ans+min(left_max,right_max)-height[i];
        }

        return ans;
    }
};

//在暴力方法中，我们仅仅为了找到最大值每次都要向左和向右扫描一次。但是我们可以提前存储这个值。因此，可以通过动态编程解决。
class Solution {
public:
    int trap(vector<int>& height) {
        int ans=0;
        int size=height.size();

        int l_max=0,r_max=0;
        vector<int> left_max(size,0);
        vector<int> right_max(size,0);
        for(int i=0;i<size-1;i++){
            l_max=max(height[i],l_max);
            left_max[i]=l_max;
        }

        for(int i=size-1;i>=0;i--){
            r_max=max(height[i],r_max);
            right_max[i]=r_max;
        }

        for(int i=1;i<size-1;i++){
            ans+=min(left_max[i],right_max[i])-height[i];
        }

        return ans;
    }
};

//双指针
//如果一端有更高的条形块（例如右端），积水的高度依赖于当前方向的高度（从左到右）。当我们发现另一侧（右侧）的条形块高度不是最高的，我们则开始从相反的方向遍历（从右到左）。
//我们必须在遍历时维护 \text{left\_max}left_max 和 \text{right\_max}right_max ，但是我们现在可以使用两个指针交替进行，实现 1 次遍历即可完成。
int trap(vector<int>& height)
{
    int left = 0, right = height.size() - 1;
    int ans = 0;
    int left_max = 0, right_max = 0;
    while (left < right) {
        if (height[left] < height[right]) {
            height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
            ++left;
        }
        else {
            height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
            --right;
        }
    }
    return ans;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73

← 链表题型 →