图 - 概述
图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中,图是最灵活的数据结构之一,很多问题都可以使用图模型进行建模求解。
图
图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成,通常表示为: G(V,E),其中,G表示一个图,V是图G中顶点的集合,E是图G中边的集合。
和线性表,树的差异:
- 线性表中把数据元素叫元素,树中将数据元素叫结点,在图中数据元素,则称之为顶点(Vertex)。
- 线性表可以没有元素,称为空表;树中可以没有节点,称为空树;但是,在图中不允许没有顶点(有穷非空性)。
- 线性表中的各元素是线性关系,树中的各元素是层次关系,而图中各顶点的关系是用边来表示(边集可以为空)。
相关概念
顶点的度*顶点Vi的度(Degree)是指在图中与Vi相关联的边的条数。对于有向图来说,有入度(In-degree)和出度(Out-degree)之分,有向图顶点的度等于该顶点的入度和出度之和。邻接- 若无向图中的两个顶点V1和V2存在一条边(V1,V2),则称顶点V1和V2邻接(Adjacent);
- 若有向图中存在一条边<V3,V2>,则称顶点V3与顶点V2邻接,且是V3邻接到V2或V2邻接直V3;
路径- 在无向图中,若从顶点Vi出发有一组边可到达顶点Vj,则称顶点Vi到顶点Vj的顶点序列为从顶点Vi到顶点Vj的路径(Path)。
连通- 若从Vi到Vj有路径可通,则称顶点Vi和顶点Vj是连通(Connected)的。
权(Weight)- 有些图的边或弧具有与它相关的数字,这种与图的边或弧相关的数叫做权(Weight)。
类型
无向图
- 如果图中任意两个顶点之间的边都是无向边(简而言之就是没有方向的边),则称该图为无向图(Undirected graphs)。 无向图中的边使用小括号“()”表示; 比如 (V1,V2);
有向图
- 如果图中任意两个顶点之间的边都是有向边(简而言之就是有方向的边),则称该图为有向图(Directed graphs)。 有向图中的边使用尖括号“<>”表示; 比如/<V1,V2>
完全图
无向完全图: 在无向图中,如果任意两个顶点之间都存在边,则称该图为无向完全图。(含有n个顶点的无向完全图有(n×(n-1))/2条边)有向完全图: 在有向图中,如果任意两个顶点之间都存在方向互为相反的两条弧,则称该图为有向完全图。(含有n个顶点的有向完全图有n×(n-1)条边)
图的存储结构
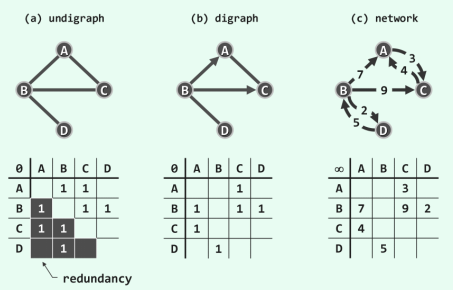
图的两种表方法,邻接表就是链表,邻接矩阵就是二维数组。
- 邻接矩阵判断连通性迅速,并可以进矩阵运算解决些问题,但是如果图⽐较稀疏的话很耗费空间。
- 邻接表比较节省空间, 但是很多操作的效率上肯定比不过邻接矩阵。
邻接表

邻接矩阵